Abstract
The out-of-plane crushing resistance of fractal-like honeycombs with self-similar hierarchy are investigated numerically and analytically. The hierarchical honeycombs are developed via replacing each three-edge vertex of a regular hexagonal honeycomb by a smaller hexagon. Hierarchical honeycombs with higher orders are constructed by repeating this process. Theoretical solutions are derived based on the Super Folding Element (SFE) theory to predict the mean crushing forces (MCFs) of the hierarchical honeycombs. Numerical simulations are also conducted in conjunction with the theoretical solutions. Crushing resistances of three groups of hierarchical honeycombs with different relative densities are explored subsequently. Good agreement between results obtained using theoretical and numerical methods indicates that the theoretical predictions are reliable. The results show that hierarchy can significantly improve the crushing resistance of honeycombs. It is found that the MCFs of first to fourth order hierarchical honeycombs are improved by 71%, 114%, 201% and 309% compared with the regular honeycomb under the same relative density, respectively. It reveals that the amplification of the MCF from one generation to the next approaches a constant (ξn=1.26) when the hierarchical order is sufficiently large. The potential maximum achievable amplifications of the MCF for hierarchical honeycombs of different relative densities are also discussed.
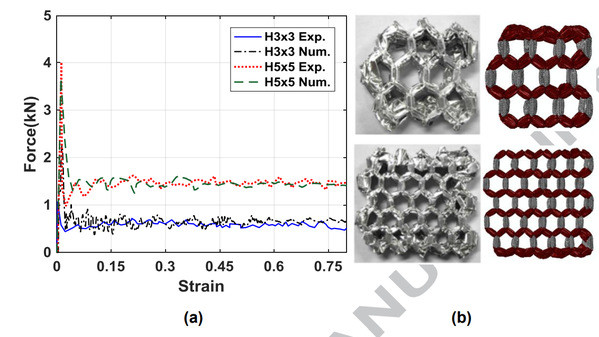
Fig. Validation of the modeling method: (a) Force-strain curves; (b) Deformation patterns.
原文链接:https://doi.org/10.1016/j.compstruct.2018.02.082


